|
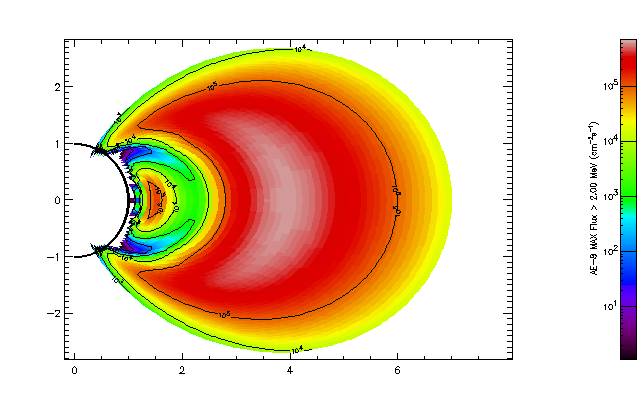
| Figure 1. Invariant coordinate map of the AE-8 MAX electron flux distribution for E > 2 MeV. |
| Table of Contents | ECSS | Model Page |
| Background Information | Background Information | |
| Invariant coordinates | ||
In a dipole magnetic field, the total field strength is given by:
| B = MR-3 [1+3 sin2(Lambda)]1/2 | (1) |
The radial and latitudinal components of the field are given in polar coordinates by:
| BR = 2 MR-3 sin(Lambda) | (2) |
| BLambda = - MR-3 cos(Lambda) | (3) |
By definition, McIlwain's (1961) L-parameter for a dipole field is the radial distance of the intersection of the field line with the magnetic equator; (Note: this is not true for a real field, where L is defined by means of a function of the adiabatic integral invariant I). In this definition of L, McIlwain used the value 0.311653 gauss RE for M.
B is the magnetic field strength, determining the position along the fieldline from the minimum B0 = M L-3 at the magnetic equator.
The equation for a dipole magnetic field line in spherical coordinates is:
| [1/R][dR/d(Lambda)] = BR/BLambda = -2 sin(Lambda) /cos(Lambda) | (4) |
Integration of this equation gives:
| R = L cos2(Lambda) | (5) |
In a non-dipole magnetic field, L is defined as a function of the adiabatic integral invariant I. R, Lambda coordinates can now be defined as:
| B = MR-3 [1+3 sin2(Lambda)]1/2 = MR-3 [ 4 - 3 RL-1]1/2 | (6) |
| R = L cos2(Lambda) | (7) |
| B0 = ML-3 | (8) |
It is clear that it is easy to compute B and L given R and Lambda. The inverse transformation however can not be accomplished in terms of well-known functions.
Substituting Equations 8 and 9 in Equation 7 gives:
| (BB0-1)2 (RL-1)6 - (4 - 3 RL-1) = 0 | (9) |
This equation can be solved numerically (e.g. with the Newton-Raphson algorithm) for RL-1. Substitution of RL-1 in Equation 8 then gives Lambda.
Note that in a non-dipolar field R and Lambda are different from the radial distance and the magnetic latitude, respectively.

|
| Figure 1. Invariant coordinate map of the AE-8 MAX electron flux distribution for E > 2 MeV. |
McIlwain, C. E., Coordinates for Mapping the Distribution of Magnetically Trapped Particles, J. Geophys. Res., 66, pp. 3681-3691, 1961.