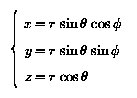
| Table of Contents | ECSS | Model Page |
| Background Information | Magnetic field models | |
| Dipole approximations | ||
It is customary to express the geomagnetic field as the gradient of a scalar potential V. The function V is usually expressed as an orthogonal expansion in spherical harmonics.
We introduce a system of orthogonal Cartesian coordinates (x,
y, z) with
origin at the centre of the Earth. The Z-axis coincides with the
Earth's rotation axis, the X-axis lies in the equatorial plane
and is directed towards the Greenwich meridian, and the Y-axis
completes the right-handed coordinate system. In this frame of reference, we
define a system of spherical coordinates (r, theta, phi) whose polar axis
coincides with the Z-axis. The transformation formulae from
Cartesian coordinates to spherical coordinates are:
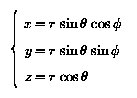
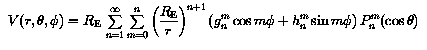
The direction defined by the Earth-centred dipole is called the geomagnetic axis. The sum of terms with n = 1 in the expansion reduces to one term in the spherical coordinate system with centre at the Earth's centre and polar axis coinciding with the geomagnetic axis. This new coordinate system (r1, theta1, phi1) is called the system of geomagnetic coordinates.
Let thetan and phin denote the
colatitude and azimuth of the point of intersection of the geomagnetic axis
with the Earth's surface in the northern hemisphere. The
transformation from
geographic Cartesian coordinates (x, y, z) to geomagnetic
Cartesian coordinates
(x1, y1, z1) is then given
by:
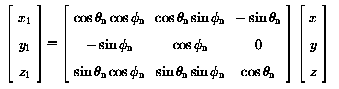
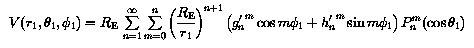
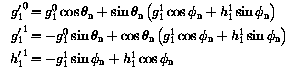
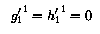
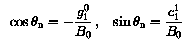
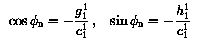
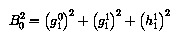
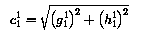
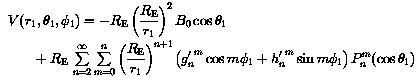
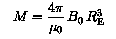
| B0 | = | 3.01153 104 nT |
| M | = | 7.788 1022 A m2 |
| thetan | = | 10.46 ° |
| phin | = | -71.57 ° |
for epoch 2000. Table I lists the positions of the northern centred dipole pole calculated with DGRF 1945-1990 and IGRF 1995-2000 .
| Model | Latitude | Longitude |
|---|---|---|
| DGRF 1945 DGRF 1950 DGRF 1955 DGRF 1960 DGRF 1965 DGRF 1970 DGRF 1975 DGRF 1980 DGRF 1985 DGRF 1990 IGRF 1995 IGRF 2000 |
78.47 78.47 78.46 78.51 78.53 78.59 78.69 78.81 78.97 79.13 79.30 79.54 |
291.47 291.15 290.84 290.53 290.15 289.82 289.53 289.24 289.10 288.89 288.59 288.43 |
It may be noted that the rectangular coordinate system used by Schmidt (1934) and Bartels (1936) differs from those now conventionally used and this circumstance has led to an erroneous designation of the dipole position in Chapman and Bartels (1940).
When reference is made to the eccentric dipole model of the Earth's magnetic field, it is now generally understood that the Schmidt (1934) criterion and its resulting mathematical formulation are applicable, even though other eccentric dipole models are possible (e.g. Bochev, 1969), and it is the Schmidt eccentric dipole model that is described here.
The dimensionless coordinate quantities xi, eta and zeta are given by:
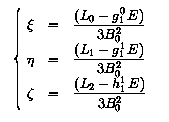
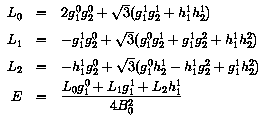
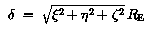
| L0 | = | 1.028 108 nT2 |
| L1 | = | -1.706 108 nT2 |
| L2 | = | 1.252 108 nT2 |
| E | = | -5.791 102 nT |
| eta | = | -0.06308 |
| zeta | = | 0.04713 |
| xi | = | 0.03149 |
The shifts in the x, y and z GEO directions are therefore -401.86 km, 300.25 km and 200.61 km, respectively, and the total distance shifted by the dipole is delta = 540.27 km. The direction of the shift is given by thetad = arccos (200.61/540.27) = 68.20°, and phid = 90° + arctan (401.86/200.61) = 143.24°, that is, it is toward the point 21.80°, 143.24°. This point is in the northwest Pacific, at the northern end of the Mariana Islands. The projection of the dipole position on the Earth's surface is shown in Figure I. Table II gives the position of the eccentric dipole for epochs 1945-2000.
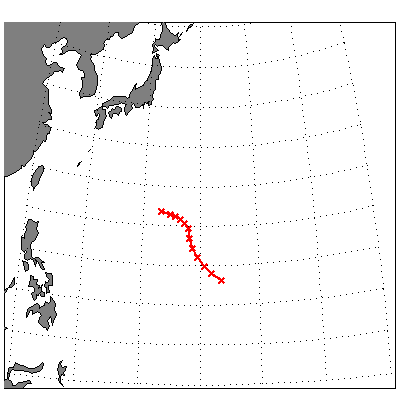 |
| Figure 1. Projection of the eccentric dipole position on the Earth's surface. |
| Model | X0 (km) | Y0 (km) | Z0 (km) | delta (km) |
|---|---|---|---|---|
| DGRF 1945 DGRF 1950 DGRF 1955 DGRF 1960 DGRF 1965 DGRF 1970 DGRF 1975 DGRF 1980 DGRF 1985 DGRF 1990 IGRF 1995 IGRF 2000 |
-355.24 -359.03 -362.59 -365.90 -368.77 -373.13 -378.57 -385.41 -391.78 -396.49 -400.51 -401.86 |
175.47 190.67 203.52 214.78 223.78 230.96 237.02 247.49 258.51 270.82 282.84 300.25 |
92.33 101.29 110.75 122.42 133.56 146.40 159.83 170.21 178.73 185.88 192.87 200.61 |
406.83 418.95 430.30 441.58 451.57 462.60 474.38 488.63 502.26 514.87 526.89 540.27 |
The eccentric dipole model for the Earth's magnetic field produces two different varieties of poles. The first of these are referred to as the axial poles (i.e. the two points on the Earth's surface where the eccentric dipole axis intersects the surface). Because of the displacement of the eccentric pole away from the Earth's centre the eccentric dipole axis and associated magnetic field, in particular, are not perpendicular to the surface at the axial poles. There are, however, two points where the magnetic field is perpendicular to the surface, which are referred to as the eccentric dipole dip poles.
The axis of the eccentric dipole is parallel to the centred dipole axis. This fact and the knowledge that the eccentric dipole axis passes through the point (eta, zeta, xi) RE in GEO rectangular coordinates enable the derivation of an expression for the axis in our basic geographic spherical polar coordinate system. The equation for a line passing through a point (x0, y0, z0) is:
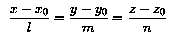
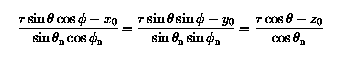
Substituting r = RE in the expression above and carrying out the appropriate algebraic manipulations, the following equations are obtained for the intersection points:
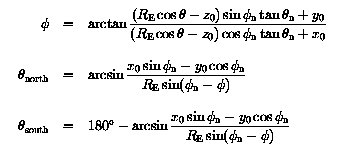
| North pole | South pole | |||
|---|---|---|---|---|
| Model | latitude (deg) | longitude (deg) | latitude (deg) | longitude (deg) |
| DGRF 1945 DGRF 1950 DGRF 1955 DGRF 1960 DGRF 1965 DGRF 1970 DGRF 1975 DGRF 1980 DGRF 1985 DGRF 1990 IGRF 1995 IGRF 2000 |
80.90 81.04 81.15 81.30 81.40 81.53 81.68 81.88 82.15 82.39 82.65 83.03 |
-83.86 -84.39 -84.94 -85.57 -86.27 -87.06 -87.99 -89.05 -90.05 -91.05 -92.20 -93.30 |
-75.52 -75.38 -75.25 -75.19 -75.13 -75.10 -75.11 -75.11 -75.15 -75.19 -75.24 -75.34 |
121.09 120.68 120.29 119.98 119.62 119.40 119.29 119.17 119.18 119.05 118.87 118.66 |
The dip poles are located on the great circle defined by the intersection of the plane containing both the centred and the eccentric axes with the earth's surface. They are separated from their corresponding eccentric dipole axial poles by small angular distances along the great circle, with the direction of the separition being away from the local centric dipole pole (All centred and eccentric poles lie on the same great circle). At these points there is enough curvature of the dipole field lines away from the eccentric dipole axis to compensate for the small angle made by the axis with the Earth's surface and thus to bring the field lines perpendicular to the surface (see figure 2).
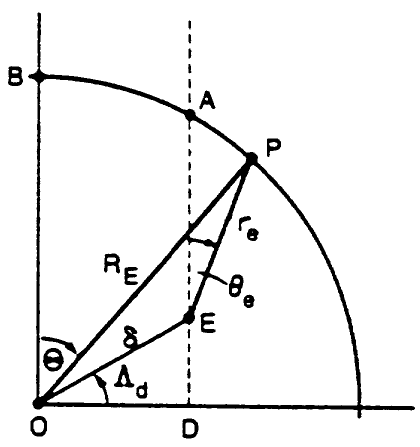 |
| Figure 2. Geometry used in the derivation of the equation for the dip poles. P is a general point and not necessarily the dipole pole. [Taken from Fraser-Smith (1987)]. |
The procedure to calculate the dip pole positions consists of the following steps:
The only significant feature in the first step is a change of the coordinates of the eccentric dipole. The eccentric dipole has CD coordinates (X0, Y0, Z0) and (delta, THETA, PHI). The change of coordinates from (delta, theta, phi) to (delta, THETA, PHI) is easily carried out with the transformation matrix described in the section centred dipole model.
The second step in the derivation is to obtain the CD azimuthal coordinates of the dip poles. Figure 2 shows the geometry required in this step of the derivation and it foolows that the CD azimuthal coordinates for the dip poles are the same and equal to PHId; the azimuthal angle does not play a further role at this stage of the derivation. The other CD coordinates of the dip poles are now obtained by resolving the magnetic field of the eccentric dipole, located at E in figure 2, along the tangent to the circle (representing the Earth's surface) at the general point P, equating the resolved field to zero, and then rearranging the resulting equations to obtain an expression for THETA. Remembering that the dipole at E is oriented along the axis DEA in figure 2, the two components of the dipole field at P are:
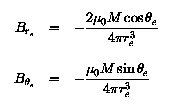
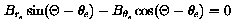
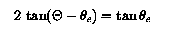
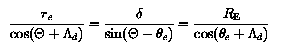
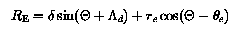
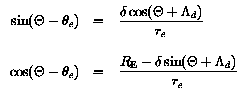
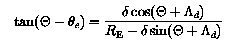
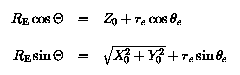
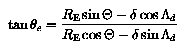
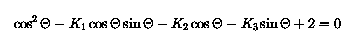
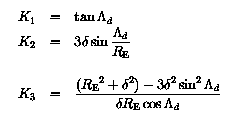
The third and final step in the derivation is to convert the CD coordinates (RE, THETA1, 2, PHId) of the dip poles into geographic coordinates using the transformation matrix described in the section centred dipole model.
Using this procedure with the IGRF coefficients for epoch 2000, the following dip pole positions are obtained:
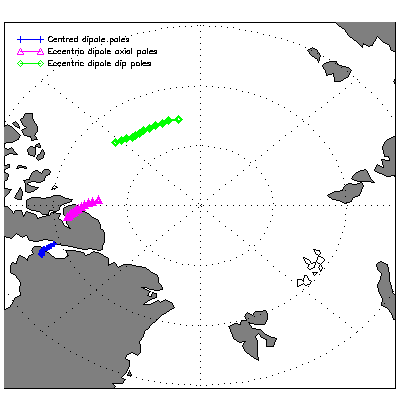 |
| Figure 3. Position of the centred dipole poles, the eccentric dipole axial poles and the eccentric dip poles in the northern hemisphere. |
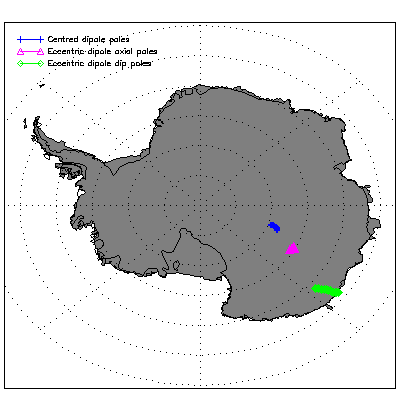 |
| Figure 4. Position of the centred dipole poles, the eccentric dipole axial poles and the eccentric dip poles in the southern hemisphere. |
| North pole | South pole | |||
|---|---|---|---|---|
| Model | latitude (deg) | longitude (deg) | latitude (deg) | longitude (deg) |
| DGRF 1945 DGRF 1950 DGRF 1955 DGRF 1960 DGRF 1965 DGRF 1970 DGRF 1975 DGRF 1980 DGRF 1985 DGRF 1990 IGRF 1995 IGRF 2000 |
82.20 82.39 82.52 82.64 82.69 82.70 82.67 82.65 82.65 82.65 82.61 82.66 |
-132.81 -135.69 -138.28 -141.07 -143.36 -145.75 -148.33 -151.89 -155.76 -159.58 -163.37 -168.60 |
-68.97 -68.56 -68.19 -67.89 -67.62 -67.37 -67.16 -66.88 -66.66 -66.44 -66.25 -66.06 |
131.79 131.09 130.49 130.03 129.59 129.38 129.32 129.18 129.12 128.86 128.57 128.04 |
Bartels, J., The eccentric dipole approximating the Earth's magnetic field, J. Geophys. Res., 41, pp. 225-250, 1936.
Bernard, J., J.-C. Kosik, G. Laval, R. Pellat, J.-P. Philippon, Représentation Optimale du Potentiel Géomagnétique dans le Repère d'un Dipole Décentré, Incliné, Ann. Géophys., 25, pp. 659-665, 1969.
Bochev, A., A dipole approximating to the highest possible degree the Earth's magnetic field, Pure Appl. Geophys., 74, pp. 25-28, 1969.
Chapman, S. and J. Bartels, Geomagnetism, vol. 2, Oxford University Press, New York, pp. 639-668, 1940.
Fraser-Smith, A. C., Centered and Eccentric Geomagnetic Dipoles and Their Poles, 1600-1985, Rev. Geophys., 25, 1, pp. 1-16, 1987.
Heynderickx, D. and J. Lemaire, Improvements to Trapped Radiation Software, Trapped Radiation Environment Model Development, Technical Note 1, ESTEC Contract No. 9828/92/NL/FM, 1993.
Schmidt, A., Der magnetische Mittelpunkt der Erde und seine Bedeutung, Gerlands Beitr. Geophys., 41, pp. 346-358, 1934.