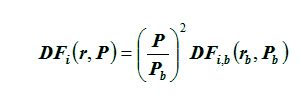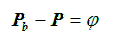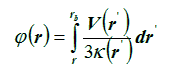Table of contents
- Introduction
- GCR particle flux models
- The ISO model
- The CREME96 model
- The CREME86 models
- The Nymmik et al. (1996) model
- Propagation of the GCR particle flux
- Geomagnetic attenuation and Earth shadowing
- References
Introduction
Galactic cosmic rays (GCR) are high-energy charged particles that enter the solar system from the outside, the flux of which becomes modulated in anti-correlation with solar activity due to the solar wind. They are composed of protons, electrons, and fully ionized nuclei. There is a continuous and isotropic flux of GCR ions. Although the flux is low, a few particles per cm2 and per s-1, GCRs include energetic heavy ions which can deposit significant amounts of energy in sensitive volumes and so cause problems to spacecrafts' electronics and humans in space. As for solar particles, the Earth’s magnetic field provides a varying degree of geomag-netic shielding of nearEarth locations from these particles.
GCR particle flux models
All the models predict fluxes for protons and Z=2 to 92 nuclei in the near-Earth space beyond the Earth's
magnetosphere.
The ISO-15390 model
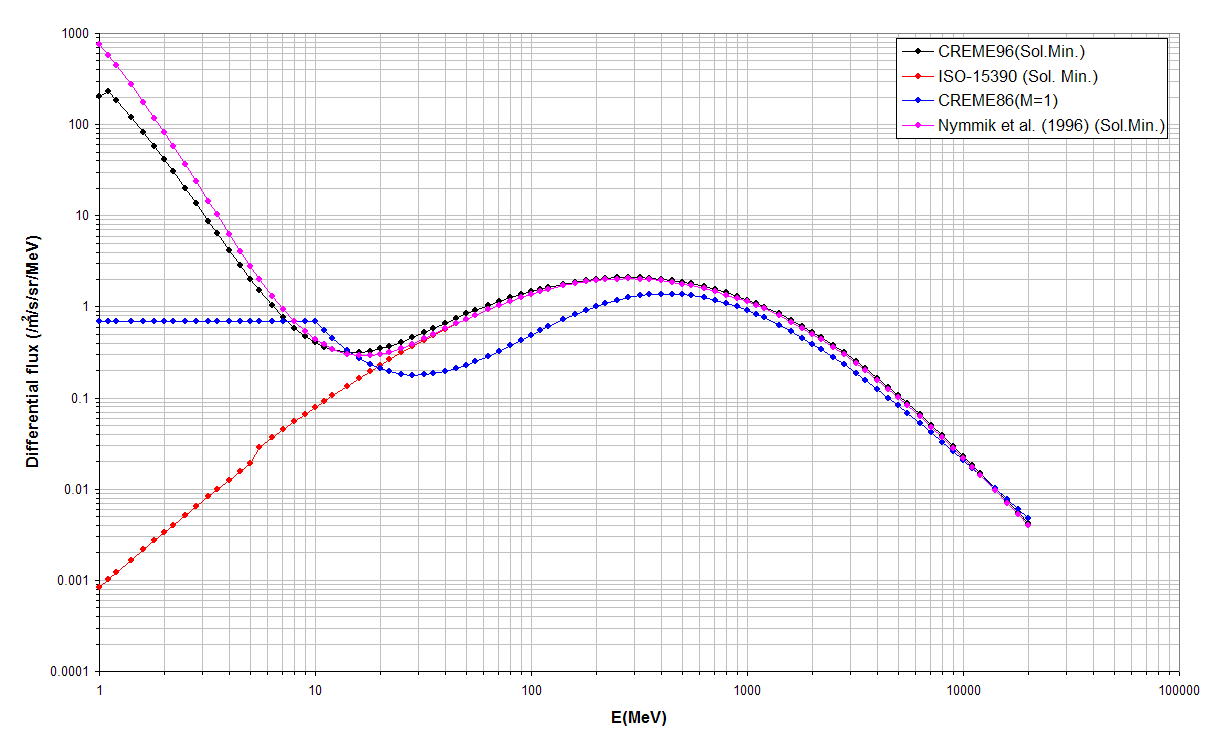
The GCR ISO model is based on the semi-empirical GCR models of the Moscow State University (MSU). All formulas and parameters needed to reconstruct the models are included in the International Standard ISO Draft 15390. To account for solar-cycle variations in the GCR intensities, 12 month averages of the Wolf(sunspot) number are used. The variations of the large-scale heliospheric magnetic field are assumed to be proportional to the variations of the Sun's polar magnetic field whose intensity and polarity are taken to be dependent on solar activity and on whether a given solar cycle is even or odd. The time lag of GCR flux variations relative to solar activity variations is taken to depend on magnetic rigidity of particles, on whether a solar cycle is odd or even, and on solar cycle phase. The model does not include anomalous cosmic rays.
The GCR CREME96 model implemented in SPENVIS is for the solar-minimum GCR environment and corresponds with the GCR maximum last observed in 1986-87. The model is based on the model of Nymmik et al. (1992) and includes anomalous cosmic ray fluxes (visible for He, N, O and Ne around 10 MeV/nucleon) derived from SAMPEX results.
The CREME86 models
The CREME86 GCR models implemented in SPENVIS are from the CREME86 software package and are marked by the interplanetary weather indices M = 1, 2, 3 and 4. The weather index M=1 gives the best approximation to the galactic cosmic ray
flux at the given date and is also included in M=2 and M=4 models. Index M=3 gives the worst-case galactic cosmic
ray fluxes that allow uncertainties in flux data and solar activity. These fluxes are so severe that they have only a 10% chance of being exceeded by actual fluxes at any moment. When M=2, the anomalous component which is assumed to be fully ionized, is added to galactic cosmic rays. When M=4, a singly-ionized anomalous component is assumed. The singly-ionized particles are affected differently than fully-ionized particles by geomagnetic cutoff. Mainly different from the CREME96 model is the solar modulation which is described by a simple sinus function: M = AsinW(t-t0)+B (W=2π/10.9 years = 0.576/year and t0= 1950.06) which is far more crude.
The Nymmik et al. (1996) model
The GCR model from Nymmik et al. (1996) is basically the same as the ISO model except that at energies below 10 MeV/nucleon the flux rises with decreasing energy.
|
|
Figure 1. The Hydrogen GCR flux near Earth predicted by the different GCR particle flux models at solar minimum.
|
Propagation of the GCR particle flux
When GCR particles enter the heliosphere they are affected by the interplanetary magnetic field and solar
wind. This results in the modulation of their total flux and differential energy spectrum as measured in the vicinity of
the Earth. The modulation varies with the varying solar activity and is often described in terms of the so-called force
field model (Gleeson and Axford, 1968; Caballero-Lopez and Moraal, 2004; McCracken et al., 2004). The model contains
one explicit parameter φ, the modulation potential, which is expressed in units of MV. The value of Zeφ corresponds to the average energy loss of cosmic rays inside the heliosphere. The underlying simplifying assumptions of the model are: a spherically symmetric and steady-state heliosphere, a negligible streaming of cosmic rays, and a radial diffusion coefficient with separable effects of heliodistance and energy/rigidity. Although these conditions are often violated, in particular on short timescales and during periods of high solar activity, the force field model provides a useful way to parameterize the shape of GCR differential energy spectrum. The differential flux DF of GCR nuclei of type i at heliodistance r (in AU) is given by:
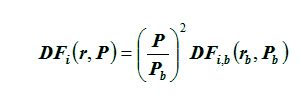
with P the rigidity P at heliodistance r and Pb at the heliospheric boundary rb. Both rigidities are related by,
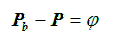
with φ the modulation potential given by,
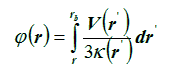
with V the radial solar wind velocity and κ the radial diffusion coefficient. For the implementation of the force field model in SPENVIS, the radial solar wind velocity is taken constant and the diffusion coefficient is considered as a constant κ0 or as a power law κ=κ0rα where the power may differ in the inner and outer heliosphere.
The GCR flux at heliocentric distance r is calculated by propagating the GCR flux (predicted by one of the GCR models) at 1 AU.
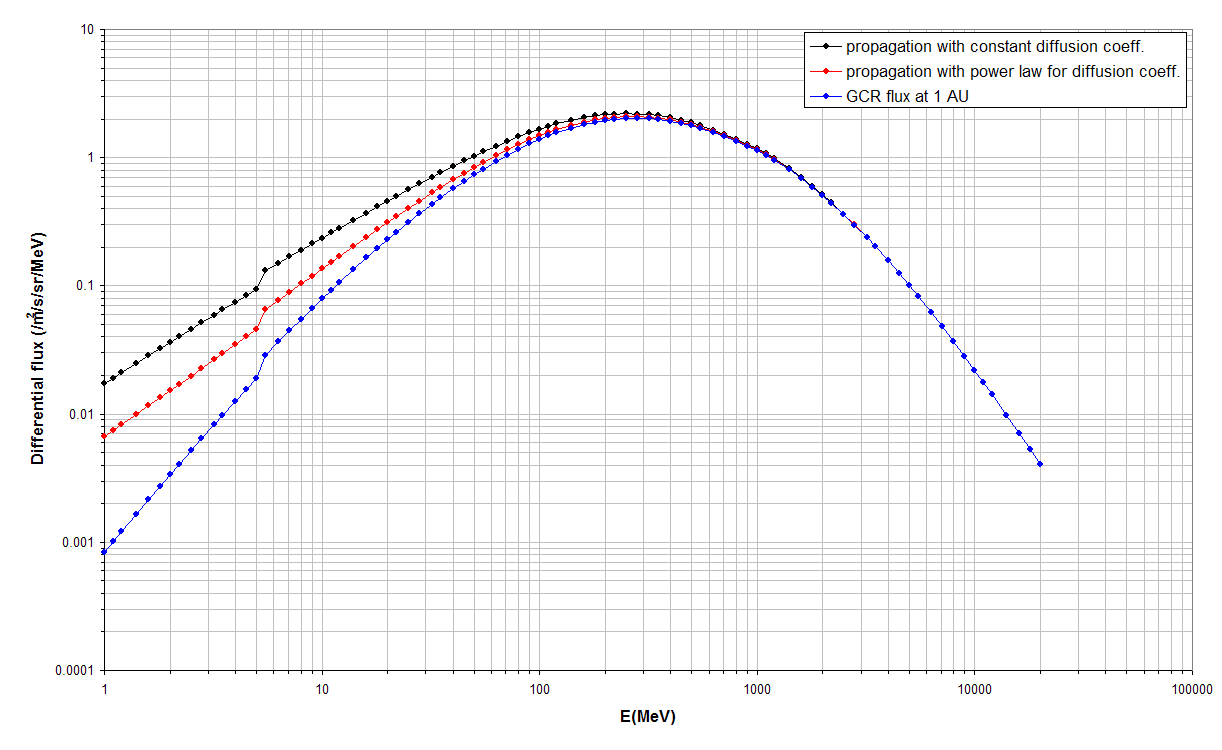
Figure 2 gives the hydrogen GCR flux near Jupiter propagated from 1 AU with the force field approximation using a constant diffusion coefficient (κ0=4.38 1022cm2/s) and a power law with a different power for the inner (α=1.1) and outer heliosphere (α=1.4). The lowest curve correspond with the GCR flux at 1 AU predicted by the ISO-15390 GCR model at solar minimum.
|
|
Figure 1. The hydrogen GCR flux near Jupiter propagated from 1 AU with the force field model, using a constant diffusion coefficient (black curve) and a power law (red curve). The blue curve is the hydrogen GCR particle flux at 1 AU predicted by the ISO GCR model at solar minimum.
|
Geomagnetic attenuation and Earth shadowing
The ability of charged particles to penetrate into the magnetosphere from
outside is limited by the Earth's magnetic field. A particle's penetrating
ability is determined uniquely by its momentum divided by its charge. For each
point in the magnetosphere and for each direction of approach to that point,
there exists a threshold value of magnetic rigidity, called the
geomagnetic cutoff.
Below this value, no charged particle can reach the specified point from the
specified direction.
As the geomagnetic cutoff varies with the particle's arrival direction, the
geomagnetic cutoff transmission is averaged over all arrival directions. For a
given location and rigidity, the
integrated solid angle from where particles with this rigidity can reach the
location, divided by 4pi, is called the attenuation or exposure factor.
The attenuation factor for each proton energy is averaged over the spacecraft
orbit and then multiplied with the interplanetary proton fluence provided by
the proton models. For a given energy, the exposure time is defined as the total
time that the orbit is in regions where the attenuation factor is non-zero.
SPENVIS provides the
attenuation for each orbital point and each proton energy, the orbit averaged
attenuation factor, and the exposure time.
The presence of the solid Earth occults part of the solid angle from which
particles can arrive at a given location. This effect is included in the
calculation of the attenuation factor.
During magnetic storms, the geomagnetic cutoff is altered, usually allowing
penetration to any given point in the magnetosphere by lower energy particles
than is normally possible. A simple expression is used to account for this
effect on the attenuation factor. Solar events are often, but not always,
accompanied by magnetic storms at the Earth. Therefore, the user has the option
of selecting a quiet or disturbed magnetosphere.
The calculation of the attenuation factor is based on a number of
approximations that limit the validity of the result. It is well established
that solar protons can penetrate much deeper in the magnetosphere than
predicted by the simple attenuation model. Therefore, the user has the option
of switching off the geomagnetic attenuation (this does not affect the Earth
shadowing effect) to have an idea of the worst case effect of solar events.
References
Adams, J. H., Cosmic Ray Effects on Microelectronics, Part IV, NRL Memorandum Report 5901,
Washington, D.C., 1986.
Caballero-Lopez, R. A., and H. Moraal (2004), Limitations of the force
field equation to describe cosmic ray modulation, J. Geophys. Res., 109,
A01101, doi:10.1029/2003JA010098.
Gleeson, L. J., and W. I. Axford (1968), Solar modulation of galactic
cosmic rays, Astrophys. J., 154, 1011.
McCracken, K. G., F. B. McDonald, J. Beer, G. Raisbeck, and F. Yiou
(2004), A phenomenological study of the long-term cosmic ray modulation
850 – 1958 AD, J. Geophys. Res., 109, A12103, doi:10.1029/
2004JA010685.
Nymmik, R.A., Panasyuk, M.I., Pervaja, T. I. and Suslov, A.A., A Model of Galactic Cosmic Ray Fluxes, Nucl. Tracks & Radiat. Meas, 20, 427-429 (1992).
Nymmik, R.A., Panasyuk, M.I. and Suslov, A.A., Galactic cosmic ray flux simulation
and prediction: Adv. Space Res., Vol. 17, No. 2, 1996.
Tylka, A. J., et al., CREME96: A Revision of the Cosmic Ray Effects on
Micro-Electronics Code, IEEE Trans. Nucl. Sci., 44, 2150-2160,
1997a.
Last update: Mon, 12 Mar 2018