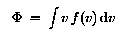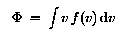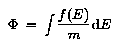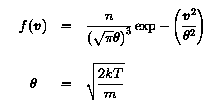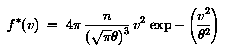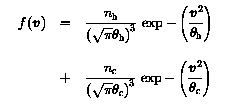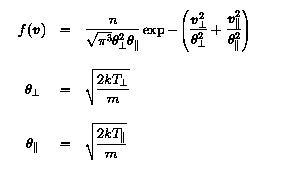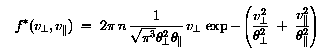Contents
Introduction
In a neutral gas or a plasma, particles move around with a variety of
velocities. Not only the absolute velocity changes, but also the direction.
Although it is hard to say what velocity an individual particle may have, it is
possible to use a statistical approach to characterize the velocity attributes.
The mathematical description of this statistical approach is called the
velocity distribution function. In general, this
distribution function has to be described in 6-d space, made up of the three
spatial vectors and the three velocity vectors, with units [s3
m-6]. In this text, we take the
definition that the integration over the three velocity components gives the
density.
Other definitions exist, such as the one used in ECSS-10-04.
There, for distributions that are spatially
uniform and isotropic,
the function is written as f(v), a function of scalar
velocity v, with units [s m-4], and to obtain the density,
integration over the scalar velocity and not over the velocity
components is necessary.
Since there is a relation between energy and velocity, i.e. E =
½ m v2, with m the mass of the particle,
the same approach can be used to describe
the energy distribution, f(E).
The distribution function can be converted to a flux by integration:
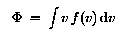or, since mv dv = dE
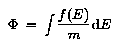
Maxwellian distribution
In thermal equilibrium, the plasma distribution function can be
described by:
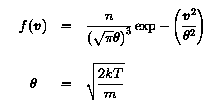with:
- n: density;
- theta: thermal speed;
- T: temperature;
- m: particle mass;
- k: Boltzmann's constant: 1.380662 10-23 J K-1.
In terms of scalar velocity v, the Maxwellian distribution becomes:
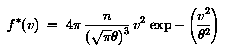
The complete distribution is described by a pair of values for density and
temperature. Even non-equilibrium can often be usefully described by a
combination of two Maxwellians or a Maxwellian and a generalized Lorentzian.
Double Maxwellian distribution
Unstable velocity distributions are non-Maxwellian distributions that have
some sort of anisotropy such as a beam, a temperature anisotropy, or an
anisotropy in pitch angle. The velocity distribution used for
a beam (i.e. a second plasma population flowing through the first), is the
simplest case and can be treated in one dimension. The distributions of both
plasmas are Maxwellian, but the overall distribution is not. This is called a
Double Maxwellian and is described by two pairs of values for density and
temperature.
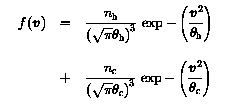where the indices "h" and "c" refer to hot and cold plasma respectively.
An example of a Double Maxwellian velocity distribution is the SCATHA worst
case environment which is used for the
assessment of surface
charging. Table 1 lists the densities and temperatures
for the SCATHA worst case charging event, where the spacecraft charged to -8 kV
in sunlight on 24 April 1979. It should be noted that although the listed ion
and electron densities are not equal, electrical neutrality is maintained by
less energetic plasma which is not involved in the charging event and so not
listed.
Table I. SCATHA Worst case charging event
| Double Maxwellian Fit |
Electrons |
Ions |
| n [cm-3] |
kT [keV] |
n [cm-3] |
kT [keV] |
| Cold plasma |
0.2 |
0.4 |
0.6 |
0.2 |
| Hot plasma |
1.2 |
27.5 |
1.3 |
28.0 |
Bi-Maxwellian distribution
Another example of an unstable velocity distribution is one in which there
is a temperature anisotropy, meaning that the temperature
characterizing the movement of the particles in one direction is different from
that of another direction. For this case, a two dimensional distribution must
be used. The coordinate system usually used consists of the parallel and
perpendicular velocities with respect to the background magnetic field. A
stable two dimensional distribution (i.e. one wich is Maxwellian in both the
parallel and perpendicular directions) is independent from the direction.
A contour plot in the plane (vparallel,
vperpendicular) will look like concentric circles.
However, if the temperature is larger in one direction than in the other, the
distribution will be oblong along the first direction. The resulting equation
becomes:
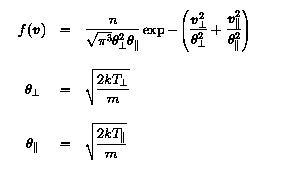In terms of the parallel and perpendicular components, this can be written as:
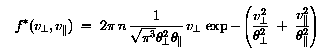
Generalized Lorentzian
Most of the time, the velocity distribution function of particles in space
plasmas has a non-Maxwellian
superthermal tail. The distribution function decreases generally as
a power law of the velocity v instead of exponentially (Bame et al., 1967). A useful function to model such
plasmas is the generalized Lorentzian (or kappa) distribution (Summers and Thorne, 1991):
When the spectral index kappa increases towards infinity, the
Lorentzian tends to a Maxwellian.
Kappa distributions have been used to analyse spacecraft data
collected in the Earth's magnetospheric plasma sheet and in the solar wind
(Scudder, 1992; Pierrard and
Lemaire, 1996).
References
Bame, S. J., J. R. Asbridge, H. E. Felthauser, E. W. Hones Jr., and I. B.
Strong, Characteristics of the plasma sheet in the Earth's magnetotail, J.
Geophys. Res., 72, pp. 113-119, 1967.
Pierrard, V., and J. Lemaire, Lorentzian ion exosphere model, J. Geophys.
Res., 101, 7923, 1996.
Scudder, J. D., On the causes of temperature change in inhomogeneous
low-density astrophysical plasmas, Astrophys. J., 398, 99, 1992.
Summers, D., and R. M. Thorne, The modified plasma dispersion function,
Phys. Fluids B, 8(3), pp. 1835-1847, 1991.
Last update: Mon, 12 Mar 2018