 |
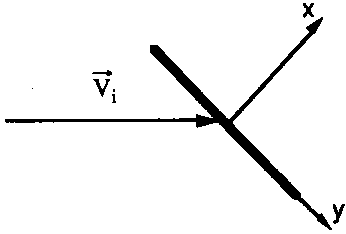
| Figure 1. Reference frame for the velocity of impacting particles |
| Table of Contents | ECSS | Model Page |
| Background Information | Atmosphere and ionosphere models | |
| Atomic oxygen erosion | ||
Space Shuttle flights (flights 5 and 8) have demonstrated that interactions between spacecraft surfaces and atomic oxygen, the major component of the low Earth orbit environment, can produce significant changes in mass and surface properties for many materials through erosion and oxidation. The orbiting spacecraft motion through the atmospheric atomic oxygen can generate a flux to the spacecraft surfaces with significant energy of about 5 eV.
The changes in surface properties are directly related to the atomic oxygen fluence or total integrated flux incident on material surfaces. This fluence in turn is dependent on many parameters such as attitude of the surface relative to the orbital velocity vector, altitude, solar activity, and life span of the spacecraft.
Assessment of the problem involves three areas:
Numerous events can occur when atomic oxygen impacts a surface [Banks and Rutledge, 1988]. The atomic oxygen may elastically scatter from the surface in a specular manner, it may energy and momentum accommodate to the surface and then be ejected in a diffuse manner, it may attach to the surface and react with other arriving species to form excited nitrogen oxide, which de-excites to cause the glow phenomenon, or the atomic oxygen may chemically react with the surface. Space tests indicate that the probability of chemical reaction of atomic oxygen with carbon is only 13%, and with silver, greater than 62% [Banks et al., 1988; Gregory, 1986]. In the case of carbon, the unreacted atomic oxygen is predominantly ejected in a diffuse or near cosine distribution with an ejection peak shifted slightly in the specular direction. The actual probability of reaction of atomic oxygen with silver may be quite high for clean silver surfaces. However, silver oxide formation may contribute to shielding of the underlying silver or may serve as a catalytic surface for reassociation of the atomic oxygen. Possible atomic oxygen reactions with polymers in low Earth orbit include hydrogen abstraction, oxygen addition to form excited radicals followed by hydrogen elimination, oxygen insertion into the C-H bonds, and replacement by formation of alkoxy radicals.
Quantification of the susceptibility of materials to oxidation from atomic oxygen interaction is made possible by the fact that most oxidation products are volatile, and measurable surface recession occurs. In cases where oxidation products remain adherent, inhibition of further oxidation usually occurs. From a spacecraft designer's perspective, quantification of atomic oxygen interaction in terms of erosion yield defined as recession per fluence (cm3 atom-1) is most useful for determining mission suitability. Banks and Rutledge [1988] present a compilation table of erosion yields of materials tested in low Earth orbit. On a microscopic level, spacial variations in erosion yield tend to give rise to a dense pillar of conelike surface morphology if the reaction products are volatile species, as in the case of organic polymers and carbon. This surface morphology is much more pronounced for ram exposed surfaces as opposed to sweeping atomic oxygen incidence. These microscopic surface features, typically ranging in size from 0.1 to several microns, give rise to changes in optical properties, the most significant of which is a dramatic increase in the diffuse reflectance with an accompanying loss in specular reflectance [Banks et al., 1988].
Space tests have shed some light on the degree to which erosion yield is dependent upon various environmental factors. The effect of atomic oxygen impact angle for Kapton and Mylar in space indicates that the rate of material recession depends on the impact angle with respect to the surface normal raised to the 1.5 power as opposed to the 1.0 power as on might expect [Visentine et al., 1985]. The effect of material temperature has been shown to influence the erosion yield of graphite, and activation energies have been predicted [Gregory, 1986]. However, the range of temperatures used for the evaluation of Kaption, Mylar, and Tedlar has been too small to ascertain any significant dependence of erosion yield upon material temperature. Space tests have not identified any significant influence of solar radiation, charged species, or polymer thickness on erosion yield [Banks et al., 1988]. Erosion yield of Kapton H due to space exposure indicates no significant dependence upon flux or fluence based on the limited information available from STS flights 3, 4, 5, and 8 [Banks et al., 1988]. Variations in the erosion yield of Kapton as a function of oxygen ion or atom energy are not available from space testing to date because the low Earth orbital configurations produce energies only in the 4-5 eV range. However, the dependence of erosion yield on impact energy is of utmost importance for the designers of ground simulation systems. An erosion yield dependence proportional to the 0.68 power of the oxygen atom or ion energy has been identified for Kapton H by means of a compilation of both in-space and ground simulation tests over a wide range of energies [Ferguson, 1984].
To facilitate accurate prediction of materials performance in low Earth orbit, one must be able either to accurately simulate the low Earth orbital environmental conditions or at least be able to quantifiably extrapolate how the performance of materials under simulated conditions relates to that which would occur in space. Identification of significant factors and the dependency of erosion yield upon these factors will clarify the suitability of various atomic oxygen simulation techniques for prediction of the long term performance of spacecraft materials in low Earth orbit. Based on the evaluation of materials tested in space, there appear to be three classes materials:
The ESABASE implementation of ATOMOX considers shadowing and scattering by other spacecraft surfaces and is capable of analysing atomic oxygen effects on a spinning satellite. These capabilities use a full geometric analysis of the satellite configuration, which is outside the scope of SPENVIS. Instead, SPENVIS uses the non-geometrical version of ATOMOX for a preliminary assessment.
The following operations have to be executed by the analysis tool at each orbital point:
The fluence is defined as the integration over time of the flux crossing a surface. The flux on a totally exposed surface is the product of the particle number density and the average velocity of the particle.
The thermal velocity is given by:
The aerodynamic velocity is the difference between the wind velocity vector
vw and the spacecraft velocity vector vs in
an inertial frame of reference:
 |
| Figure 1. Reference frame for the velocity of impacting particles |
If the inward surface normal defines the direction of the x axis (see
Fig. 1), one has to calculate the average velocity component
vx of particles having vx>0:
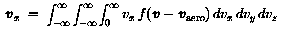
Banks, B. A., S. K. Rutledge, J. E. Merrow, and J. A. Brady, Atomic Oxygen Effects on Materials, Proc. NASA/SDIO Joint Workshop on Space Environmental Effects, Hampton, VA, 28-30 June, 1988.
Ferguson, D. C., The Energy Dependence of Surface Morphology of Kapton Degradation Under Atomic Oxygen Bombardment, Proc. 13th Space Simulation Conference, Orlando, FL, 8-11 October, 1984.
Gregory, J. C., Interaction of Hyperthermal Atoms on Surfaces in Orbit: University of Alabama Experiment, Proc. NASA Workshop on Atomic Oxygen Effects (ed. D. Brinza), Pasadena, CA, 10-11 November, 1986. (JPL Pub. No. 87-14)
Visentine, J. T., L. J. Leger, J. F. Kuminecz, and I. K. Spiker, STS-8 Atomic Oxygen Effects Experiment, Presented at the AIAA 23rd Aerospace Sciences Meeting, AIAA-85-0415, Reno, NV, 14-17 January, 1985.