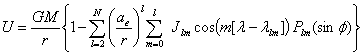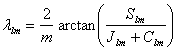D.1 Gravity models: background
Equation (4‑4) can be rewritten in terms of amplitude Jlm and phase angle λlm of individual contributions of the spherical harmonic functions to the geopotential.
|
|
(D-1) |
The equivalence of 
and 
is governed by the following equations.
|
|
(D-2) |
|
|
(D-3) |
|
|
(D-4) |
|
|
(D-5) |
For m 
l, the terms 
are called tesseral harmonics. These components divide the
Earth’s surface in a checkerboard pattern of hills and valleys, the amplitude
and phase of which are determined by the associated coefficients 
.
For l = m, the functions 
= 1,0. These terms are
called sectorial harmonics. They divide the spherical surface into
longitude-dependent sectors, similar to the segments of a basket ball.
For m = 0, the only
remaining terms 
(where
is mostly abbreviated as 
) are called zonal harmonics. They divide the spherical
surface into purely latitude-dependent bands of toroidal hills and valleys,
with Earth oblateness (
) as the dominating contribution. reflects the
equilibrium response of a rotating, elastic Earth under the influence of
centrifugal and gravitational forces. For the model EIGEN-GL04C the resulting
Earth ellipsoid has an equatorial radius of 
(may slightly vary
with the selected geopotential model), a polar radius of 
(may slightly vary
with the selected geopotential model), and an oblateness of 
.
By convention, the central
attraction term of a spherical body of uniform mass distribution is 
. If the centre of mass coincides with the origin of the
body-centred coordinate system, then 
. If the body-fixed coordinate axes furthermore coincide with
the axes of the main moments of inertia, then 
.
In order to develop a
geopotential model it is necessary to measure the gravitational acceleration
directly or indirectly, and estimate the set of model coefficients (GM, 
, ) in a least squares sense on the basis of an adequately
large number of such measurements. Direct measurements of the gravity potential
are difficult, and typically involve highly sensitive gradiometers that measure
the acceleration gradient. Indirect measurements of the gravity potential are
obtained from precise tracking data for Earth orbiting satellites. Because of
the difficulties of collecting global gravity measurements on land or sea,
relevant global geopotential models did not exist before the days of artificial
Earth orbiting satellites, and only the first few degree and order terms were
known with some accuracy.
However, a revolution in gravity model development has occurred after the year 2000, in the form of the three dedicated gravity field missions: CHAMP, GRACE and GOCE (expected to be launched in 2008). All three satellites employ precise global tracking via GPS, allowing continuous high quality orbit determination, and measure the gravity acceleration directly. The arrival of these dedicated gravity missions has essentially rendered any earlier gravity model obsolete. GRACE-only models of 360×360 resolution in degree and order (about 1°×1° patches, with ~100 km resolution on the Earth’s surface) have demonstrated to be superior to any of the earlier combined models, even if these were based on the accumulated satellite data sets from three preceding decades. The GRACE models are accurate enough to investigate the temporal variability of the gravity field, for instance due to seasonal displacements of water masses.